Wege ins Chaos
Das Lorenz-System als periodisches System
Das Lorenz-System zeigt einen interessanten Weg ins Chaos, der als Krise und Intermittenz bzw. Pomeau-Manneville-Szenario bezeichnet wird.
Der Attraktor des Lorenz-Systems durchläuft starke qualitative Veränderungen auf dem Weg ins Chaos. Diese Veränderungen deuten sich in der Nähe von Phasenübergängen durch Intermittenzen in den Zeitreihen an, bei denen ein einfacher periodischer Grenzzyklus zunehmend „aus dem Tritt gerät“, bis er sich beim Überschreiten der Grenze zum Chaos völlig verändert hat.
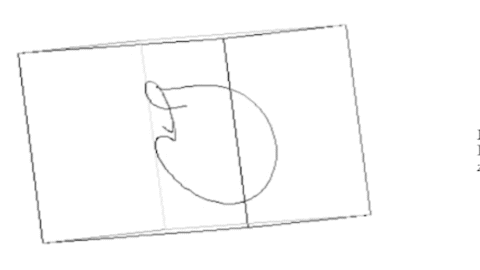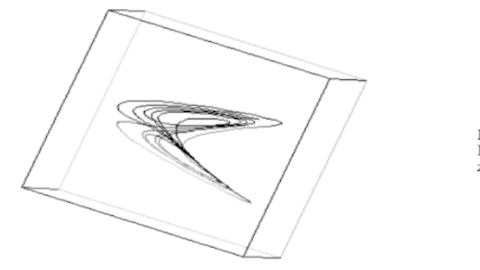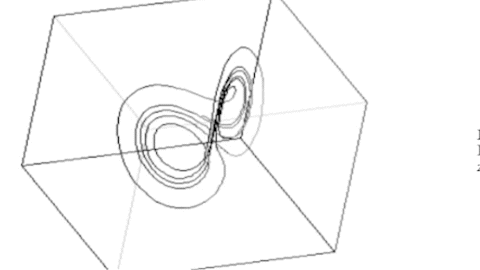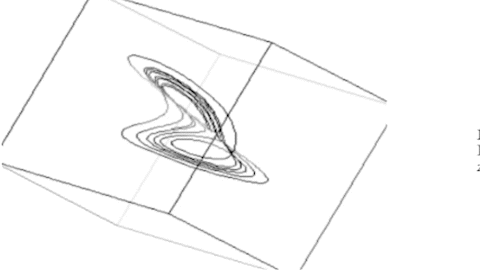
Die Animation zeigt das Lorenz-System für r = 350. Der einfache Grenzzyklus lässt die spätere (chaotische) Form noch nicht erahnen.
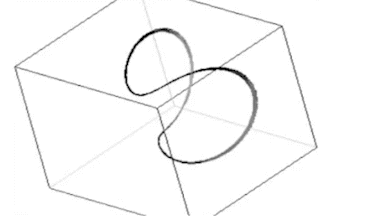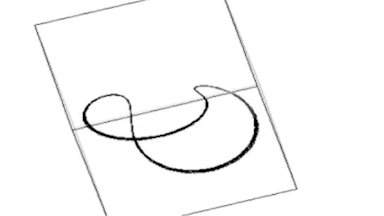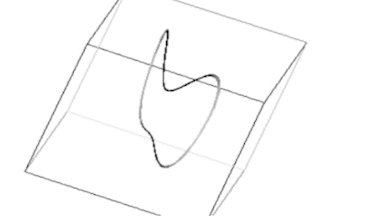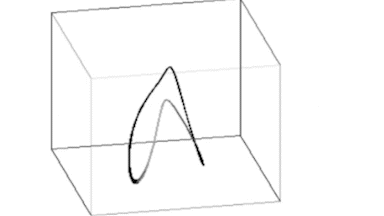
Die
generierenden Gleichungen lauten:
![]()
![]()
![]()
Periodenverdopplung
Wird r verringert kommt es zunächst zu Periodenverdopplungen.
Die Animation zeigt das Lorenz-System für r = 166. Der Grenzzyklus hat seine Periode verdoppelt.

Übegang zum Chaos
Das Die Animation zeigt das Lorenz-System für r = 120. Das Verhalten wird zunehmend komplexer und die reguläre, zyklische Gestalt verliert sich.
Chaos
Die Animation zeigt das Lorenz-System für r = 29.
Das Verhalten ist nun chaotisch.
